"It is NOT an issue of either or, Mars, Moon, Asteroids, each is as important to the other as the legs of a three legged stool…"
— Dennis Wingo, author of
Moonrush.
I like Wingo's 3-legged stool metaphor. Space advocates have been divided into warring camps, each fighting for their version of a 1 legged stool. And 1-legged stools are doomed to topple. Space advocacy is already a small voice and its influence is watered down even more by this division.
The One Legged Stool to Mars
The chief 1-legged stool guy has been Bob Zubrin. For decades he's been saying we should go straight to Mars. Messing around with the moon and asteroids are a waste of time and money in his book.
In
The Case For Mars, Zubrin advocates going to Mars in Heavy Lift Vehicles (HLVs) capable of 140 tonnes to Low Earth Orbit (LEO). Much like the Saturn V of the Apollo era. And, also like the Saturn V, expendable. Saturn V's low flight rate and high development costs resulted in
an approximately 10 billion dollars per launch price tag.
HLV apologists say a modern monster rocket would cost less since we now have decades of experience. But the recent Constellation program was
over budget and behind schedule. Nor is the current SLS any better. It looks like the SLS HLV will still have high development costs and low flight rate. John Strickland estimates each flight will have
a price tag of $14.3 billion.
On page 69 of the
The Case For Mars, Zubrin suggests 3 HLV launches per earth-Mars synodic period (about 2.14 years). That could come to more than $52 billion each launch window or $25 billion per year. The launches alone would exceed NASA's entire annual budget (around $18 billion/year as of this writing).
Not that I'm a Mars hater. In various forums I have defended the notion of humans living on Mars and other places in space. Skeptics will say humans aren't evolved to live in such environments. I reply man's
extended phenotype (clothes, fire, shelter) has enabled humans to live in northern Europe, Siberia and the Arctic. Places quite different from the environment man evolved in. The naysayers unfailingly state the painfully obvious: Mars is more hostile than northern Europe. I also state the painfully obvious: our modern extended phenotype is much more sophisticated than the animal skins, mud huts and wood fires that enabled our ancestors to settle colder climes.
And I've played the role of naysayer. While our 21st century extended phenotype is more sophisticated, it's also high maintenance. Many would be space colonizers suffer from
Home Depot Syndrome. Need a grow light? Go to Home Depot. Thermostat? PVC pipe, electric cord, duct tape, faucet, float valve, WD-40? Home Depot. This stuff is so easy to get that we forget it comes from an extensive planet-wide mining, manufacturing and transportation infrastructure that's taken centuries to build.
Charlie Stross
looks at the number of people needed to maintain our modern extended phenotype. It remains an open question how many people and how much infra-structure it would take to make a self-sufficient colony on Mars. But it's safe to say a few decades of Mars Direct style missions wouldn't do it. After 20 or 30 years we would still have an outpost almost wholly dependent on earth.
No matter what era we're in, there's always a budgetary crisis. A high profile, expensive program like Zubrin's Mars Direct would be a lightning rod for politicians looking to trim fat. I would give the program five presidential terms tops. More likely one, just as Apollo bit the dust shortly after Kennedy.
In a best case scenario, Zubrin's Mars Direct would give us abandoned flags and footprints (like Apollo). Maybe a few empty habs gathering dust. But it would cost much more than Apollo. Worst case: the hugely expensive mega rocket program will founder and collapse before even leaving low earth orbit.
The One Legged Stool to the Moon
Paul Spudis is the chief cheerleader for a one-legged moon stool.
There are volatiles in the moon's polar cold traps. But how much? One optimistic estimate says
600 million tonnes of water at the north pole in the form of water ice sheets two or more meters thick. Spudis says "If you convert that to liquid hydrogen and liquid oxygen to launch a rocket ... that is the equivalent of a space shuttle launch every day for 2,200 years." As I.S.S. astronaut Don Pettit notes, lunar propellent has the potential to break the
tyranny of the rocket equation. An abundant extra-terrestrial propellent source could make space travel routine in the earth moon neighborhood. Propellent depots at various places would break delta V budgets into manageable chunks making inexpensive,
reusable spacecraft possible.
We have extensive and valuable infra-structure in earth orbit: communication satellites, GPS, weather sats, and more. Spudis notes routine cislunar travel would make maintaining and growing orbital infra structure less costly. But does easier access to our orbital assets justify an expensive lunar propellent mine? This seems unlikely.
But there are other possible uses for lunar volatiles.
The moon is close to Earth-Moon Lagrange 1 and 2 (EML1 and EML2).
In terms of delta V, these two locations are much closer to Mars as well as the Near Earth Asteroids (NEAs). The moon could ship air, water for radiation shielding and drinking, as well as propellent to a staging platform at EML2. A fully stocked and fueled Mars Transfer Vehicle departing from EML2 has a much better chance of success than the same ship departing from LEO.
Asteroid mining and human Mars exploration could provide the needed market for lunar volatiles.
Planetary Resources or
Deep Space Industries are potential customers for a lunar propellent mine. You would think Paul Spudis would support research and development that improves their chances for success. But
he attacks the proposed Asteroid Redirect Mission (ARM).
ARM is based on the
Keck study for asteroid retrieval. Co-authors include
Chris Lewicki of Planetary Resources,
John S. Lewis - author of
Mining the Sky and
Don Yeomans as well as other scientists and engineers with impressive track records. The study shows a moderately sized spacecraft could park a 7 meter rock in high lunar orbit. The delta V for parking a rock like 2008 HU4 would be around .17 km/s. If high ISP Hall thrusters are used, the needed propellent mass isn't prohibitive. The ship could be launched on an Atlas V.
A robust Solar Energy Propulsion (SEP) vehicle would be useful for other things besides bringing rocks to the earth-moon neighborhood. Dennis Wingo has noted such a vehicle would be useful for ferrying payloads from LEO to an orbit closer to the moon.
The proposed SEP vehicle could also deflect hazardous asteroids. This is a point Paul Spudis contests. He claims "Hazardous asteroids are simply too big (many kilometers across) for such an approach."
The
Chicxulub rock, thought to wipe out the dinosaurs, is estimated at 10 kilometers. Are dino-killer sized rocks the only hazardous asteroids? Absolutely not.
The
Chelyabinsk Meteor was estimated to be 20 meters in size. About 1,500 people had to seek medical attention, mostly from broken glass. The property damage was estimated to be $33 million dollars.
The
Tunguska rock was thought be be 60 meters to 90 meters in size. The explosion knocked down 80 million trees over 2,150 square kilometers. This would be a circle 52 kilometers (32 miles) in diameter.
Paris is 105.4 square kilometers.
Chicago is 606.1 square kilometers
New York City is 1,213 square kilometers
Seattle is 369.2 square kilometers.
A Tunguska sized rock could easily wipe out a major city.
Moreover, Tunguska and Chelyabinsk sized rocks are millions of times more common than Chixculub sized rocks. Arguing the Keck SEP vehicle would be useless against Chixculubs is like arguing patching a roof is useless against tornadoes. Never mind that a sound roof is good protection against ordinary rainstorms which are far more common than tornadoes.
Besides Spudis, another well known moon guy is Dennis Wingo. The quote from the top of the page is by Wingo: "It is not an issue of either or, Mars, Moon, Asteroids, each is as important to the other as the legs of a three legged stool".
Surprisingly magnanimous and reasonable coming from hard core moon guy, right? Well, here is Wingo's version of mining asteroids:
John S. Lewis is perhaps the best known asteroid mining advocate. In Wingo's
Moonrush J. S. Lewis is quoted a lot. Wingo repeats Lewis' observation that many asteroids are metal rich and that some have very high concentrations of platinum group metals (PGMs).
Then Wingo goes on to say 3 or 4% of the moon craters come from metallic asteroids.
Wingo talks about
Barringer Crater on planet earth. He cites models that indicate the Barringer meteorite hit the earth somewhere between 16 and 20 km/s. He also cites models that indicate most of the Barringer meteorite wasn't vaporized.
The Barringer Meteorite may not have been vaporized. But it was blown into many small bits and scattered far and wide. Daniel Barringer was a wealthy mining engineer. He bet his fortune that the Barringer meteorite could be profitably mined.
Barringer lost his shirt, as did the unlucky investors who placed their bets on Barringer's scheme.
It is thought that the rich mineral deposits at Sudbury Astrobleme might be meteoritic in origin. On page 94 of
Moonrush Wingo has a graphic showing Cu-Ni-Pt-Pd mines along the edges of the Sudbury site. If the minerals are meteoritic in origin, they look like they've been scattered and mixed with the earthly rocks and dirt at the impact site. It is likely the asteroid had richer ore before it became a well smashed meteorite.
Wingo also mentions the Vredefort impact in South Africa. Ores from these mines may contain 5 to 10 ppm PGMs. There are some meteorites with a 100 to 200 ppm PGM contents. Ore becomes less concentrated after impact.
Wingo points out the moon has a shallower gravity well than earth. Therefore meteorites can strike at lower velocities. But the moon doesn't enjoy an atmosphere as earth does. Many earthly meteorites strike the earth at
terminal velocity. Mars' atmosphere can also slow a meteorite before impact. The presence of intact iron meteorites sitting on the surface of earth or Mars doesn't demonstrate such objects are sitting on the moon's surface.
On pages 100 and 101 Wingo attempts to estimate impactor velocities on the moon. He cites http://cmex-www.arc.nasa.gov/CMEX/data/SiteCat/sitecat2/crater.htm which evidently is no longer online. He also cites
this pdf. The graph on page 101 of
Moonrush gives the average impact velocity as 16.1 km/s. But this average is skewed by a small number of high velocity impacts. Wingo believes a lot of asteroids hit at speeds ranging from about 6.5 to 16 km/s.
On
his blog Wingo confidently asserts "The peak of the gaussian curve for lunar impacts is between 14.1 - 16 km/s. Only comets and high inclination rocks hit at over 20 km/sec" But
this pdf says the average lunar impact velocity is 20 km/s (fig 3 top of page 7).
It is easy to show Wingo is wrong about only comets and high inclination rocks hitting at over 20 km/s. Consider Asteroid 2011 CP4. With a semi-major axis of .911 a.u., not many would call this rock a comet. Nor does it have a big inclination, it is tilted 9.44 degrees from the ecliptic.
But 2011 CP4 has an eccentricity of .87. This jacks up the
flight path angle when it's crossing earth's orbit. When it passes through our neighborhood, 2011 CP4's velocity wrt earth is around 30 km/s.
Not wanting to trust Wingo or his cites, I constructed my own histogram:
I was surprised when my own efforts gave results not that much different from Wingo's guesstimates.
To make the histogram, I went to
JPL's NEA orbital elements page and downloaded all the NEAs that were listed as of July, 2013. I eliminated those with a perihelion > 1 a.u. or an aphelion < 1 a.u. -- these don't cross earth's orbit. With the vis viva equation it's easy to get an asteroid's speed when it's 1 a.u. from the sun. This speed plus flight path angle and inclination must be considered to find an asteroid's speed wrt earth. This speed is called Vinfinity wrt earth or V
Inf_Earth.
When the asteroid comes within earth's sphere of influence its path can be modeled as a hyperbola wrt earth. The hyperbola's speed is sqrt(V
Esc_Earth2 + V
Inf_Earth2). At lunar altitude, earth's escape velocity is around 1.5 km/s. So when the rock comes near the moon's neighborhood it's moving sqrt((1.5 km/s)
2 + V
Inf_Earth2). This is V
Inf_Moon or Vinfinity wrt the moon. An asteroid is traveling a hyperbolic orbit about the moon's center when it impacts. So impact velocity is sqrt(V
Esc_Moon2 + V
Inf_Moon2). On the lunar surface V
Esc_Moon is about 2.4 km/s.
How much is a metallic asteroid scattered when it hits at 3 to 4 km/s? Or at 8 - 9 km/s? To be honest I don't know. More intact than the Barringer meteorite is a safe bet. Wingo is probably right that there are intact platinum rich meteorites in some of the moon's craters.
But which craters? Of the 3 to 4% that come from metallic asteroids, which of those are from low speed impacts?
In
this post, Will Baird, a member of the Luna X-Prize Team Phoenicia, argues just the prospecting alone would cost a fortune. Unless space transportation becomes much more economical,
looking for needles in the lunar haystack isn't affordable. Baird's argument holds for metal prospecting. However there's some evidence of lunar water ice deposits. And, unlike lunar metal, we know exactly where to look for lunar ice.
Planetary Resources is hoping it will be able to spot the metallic and platinum rich asteroids with Arkyd probes. This would be looking for needles
not buried in the lunar haystack.
Wingo talks about revisit times. Opportunities for low delta V trips to an asteroid are rare and trip times are long. This was my major objection against the asteroids. Then I saw the
Keck study. The study shows .17 km/s suffices to nudge some asteroids from a heliocentric to a high lunar orbit.
Once an asteroid is parked in lunar orbit, revisit times are no longer an issue. Just like the moon, launch windows would open every two weeks and trips times are less than a week.
Wingo argues even at ~.2 km/s, retrieving a 100,000 tonne asteroid would be more ambitious than multiple trips to the moon. But the Keck report doesn't talk about retrieving asteroids this large, more on the order of 500 tonnes. Not only is it impractical to retrieve larger rocks, but there are also safety issues as described on page 15 of the Keck report.
The One Legged Stool to NEAs (Near Earth Asteroids)
I believe water will be the first and most valuable extra-terrestrial resource. With off-earth propellant we can break the
tyranny of the rocket equation. So long as the rocket equation mandates large disposable rockets, transportation expense will prevent profitable space mining. Two possible propellant sources are the lunar cold traps and water rich NEAs. In another post I look at
Lunar Ice vs NEO Ice.
Delta V is the major selling point for near earth asteroids. But there are other important metrics: Trip times. Light latency lag. Frequency of launch windows. This last one is a major obstacle for the more accessible NEAs.
Frequency of launch windows.
Above is an illustration of a fictitious comet I have named after Dr. John DeLaughter, who was arguing asteroids would be a better source of water ice than the moon.
This comet has a 1.9 a.u. semi-major axis, 0º inclination and a 1 a.u. perihelion. Although I believe Comet JohnD would be too warm to keep water ice for long, I granted this for the sake of argument.
From LEO, reaching Comet JohnD takes 5 km/s, less than what it takes to reach the moon from LEO (6 km/s).
About 1.3 years before John D is due to pass near the earth, a payload can be nudged into an orbit that will graze earth's atmosphere at perihelion. Courtesy aerobraking, return trips take almost no delta V. Seemingly, this asteroid would have a huge advantage over the moon.
But at JohnD's next perihelion, earth will have moved 223 degrees from the perihelion neighborhood. The right part of the illustration above shows earth's position at each perihelion. The earth doesn't revisit the comet until 22 periods later, about 58 years.
If a mine's commodity can only be delivered to market every 58 years, it's not viable.
And with rare launch windows, it would take longer to establish infra-structure. Let's say it takes three trips to plant the mining infa-structure. With launch opportunities 58 years apart, that'd take 174 years!
Dr. DeLaughter maintains establishing an asteroid mine could be done in a single trip. This is a variation on the Home Depot Syndrome I mentioned above in the Mars section. Broken thermostat? Home Depot! Broken drill bit? Any replacement part? Go to your local Asteroid Home Depot!
Moreover, mankind has millennia of experience mining at 1 g and 1 atmosphere. We have zero experience mining in vacuum and microgravity. It will be a trial and error learning process. When unexpected problems crop up, new equipment will have to be designed to deal with it. Establishing a mine will take more than one trip.
Of course a lunar mine would have similar issues. We have no experience mining in 1/6 g and vacuum. Or the deep cryogenic temperatures at the lunar cold traps. A lunar mine would need replacement parts. It's obvious establishing and maintaining a lunar mine would also take multiple trips. But lunar launch windows open every two weeks and trip times are less than a week. Three trips to the moon would not take 174 years.
Trip times and light lag latency
Asteroids in the main belt can have more frequent launch windows. Some, like 24 Themis, seem to have water ice. 24 Themis launch windows open each 1.22 years. Much worse than the moon's windows each two weeks. But not nearly as bad as Comet JohnD's windows each 58 years.
Trip time to 24 Themis is about 1.5 years. We are still a ways off from life support that's trouble free for years at a time. There is also the radiation issue. These are the same problems that make human travel to Mars so difficult. Human miners on 24 Themis won't be plausible for some time to come.
Without humans, the mining infra-structure would be built by telerobots. Light lag latency to 24 Themis would range from 68 to 35 minutes. In contrast, lunar light lag latency is about 3 seconds.
For good dexterity and sensory data, a telerobot needs good bandwidth. Signal strength falls off with inverse square of distance. Given a comparable power source, the lunar signal is anywhere from 1600 to 800 times stronger than a signal from 24 Themis. Given much better bandwidth and only 3 second light lag latency, lunar telerobots would be much more able.
Dr. JohnD maintains autonomous robots can mine the asteroids. The mining entity Rio Tinto uses autonomous robots.
This link shows Rio Tinto hauling trucks transporting dirt from one location to another. The trucks travel well maintained, predictable routes. Most of the mining environment isn't nearly as controlled and predictable as the roads this truck uses. Other Rio Tinto mining equipment such as shovels are still human controlled. And the "autonomous" trucks are closely monitored. And, whether human operated or "autonomous", humans maintain
all the equipment. The notion of autonomous robots that don't need humans nearby is almost as silly as the Asteroid Home Depot that provides any and all replacement parts.
Asteroid Delta V not always so small
Compared to main belt asteroids, the moon has better delta V!
Many believe travel to
any asteroid takes little delta V due to their shallow gravity wells. This is wrong. Going from one heliocentric orbit to another requires a change in speed. For this, an asteroid's shallow gravity well doesn't help.
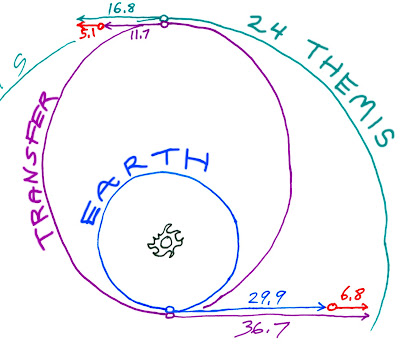
The transfer orbit to 24 Themis would have perihelion velocity 36.7 km/s and aphelion velocity 11.7 km/s. Earth travels about 29.9 km/s and Themis about 16.8 km/s. The delta V at earth's end is mitigated by the Oberth effect -- departing from LEO takes 5.2 km/s. But no Oberth benefit at the Themis end. Arriving or departing from 24 Themis takes 5.1 km/s. From LEO to Themis, total Delta V is 10.3 km/s.
Even so, Dr. DeLaughter believes reaching lunar ice would take more delta V than 24 Themis. He asks "how much delta V does it take to land on the Moon's South Pole? ... It is a lot more than a simple equatorial descent..."
For DeLaughter's benefit I described a
6.4 km/s route to the lunar poles that takes 6 days.
The first step in my route is a 3.1 LEO burn. Dr. DeLaughter
immediately challenged my number:
De Laughter cites
Lance Benner's 6.0 km/s figure for LEO to rendezvous with the moon. DeLaughter was skeptical when I pointed out 6 km/s was from LEO to
landing on the moon.
Using the vis-viva equation I calculated the transfer orbit's perigee velocity as well as a low earth orbit velocity. DeLaughter didn't seem to understand the vis-viva equation.
I provided a
Wikipedia article saying LEO to lunar surface is 5.93 km/s.
A LEO burn to reach lunar height is known as Trans Lunar Injection or TLI. I gave DeLaughter
this cite saying the Apollos' TLIs ranged from 3.05 to 3.25 km/s.
It's common knowledge that escape velocity near earth's surface is around 11 km/s. I mentioned to Dr. DeLaughter that a 6 km/s burn added to a LEO's 7.7 km/s sums to 13.7 km/s which is greater than escape velocity. This hyperbolic orbit wouldn't even have an apogee. 13.7 km/s is almost enough for Trans Jupiter Injection.
DeLaughter pointed out vectors aren't scalar quantities. Depending on their directions, a 6 km/s vector added to a 7.7 km/s
vector doesn't have to sum to a 13.7 km/s vector. To add two vectors,
take the second vector's foot and place it on the first vector's head.
Now draw a vector from the first vector's foot to the second vector's
head. This third vector is the sum of the first and second vector.
When making a 32.7º plane change, a 6 km/s burn vector added to LEO's 7.7 km/s can indeed give an ellipse with an apogee at lunar height.
But plane changes are cheaper at apogee. DeLaughter seems unaware apogee raising LEO burns are done in the same direction as the LEO velocity vector.
Unlike DeLaughter, Benner is skilled in orbital mechanics. It's safe to say Benner's 6.0 km/s figure doesn't refer to a TLI with a 32.7º plane change.
To support his 6 km/s, at one point DeLaughter gives a "grand tour" route to lunar orbit:
DeLaughter seems to forget the 3.1 km/s figure he challenged was for a TLI burn, not getting to lunar orbit. Getting to lunar orbit would require a TLI (Trans Lunar Injection) burn as well as LOI (Lunar Orbit Injection) burn. Generally these two burns total about 4 km/s.
And his "grand tour of cislunar space" is a horribly silly way to get a delta V figure. JohnD is from Texas so I will use his method to get the miles from San Antonio to Houston:
A normal person would say it's about 200 miles from San Antonio to Houston using the Interstate10. But using JohnD's method we can do a crazy path that gives us a grand tour of the Houston area. We can stop at Belville, Conroe and various surrounding communities. If we include enough towns in this crazy grand tour, it demonstrates that one can easily travel 300 miles from San Antonio to Houston.
So far as I know, Dr. DeLaughter still believes he has demonstrated my 3.1 km/s TLI figure is wrong. What he has actually demonstrated is his complete incompetence in orbital mechanics and simple physics.
Dr. DeLaughter has made other silly arguments but right now I don't have the time to address them. Suffice it to say he isn't credible.
Possible Synergies
If Planetary Resources establishes mines in lunar orbit, that would be a substantial infra-structure within spitting distance of the moon -- both in terms of kilometers and kilometers/second. A platform so close to the moon would make the moon more accessible. Infrastructure in luna orbit also makes the propellant and life support volatiles in the lunar cold traps more desirable.
The retrieval vehicle described in the
Keck study uses xenon ion drives. At first glance it seems unar water would be little help fetching rocks. But page 29 of the Keck Report says the spiral from LEO to earth escape would take 2.2 years and 3.8 tonnes of xenon. And much of the spiral is a slow trip though earth's harsh Van Allen Belts. An Earth Departure Stage (EDS) driven with lunar hydrogen/lox would take 2.2 years off mission time and increase by almost half the amount of xenon available for moving an asteroid.
The EDS could attach to a rock fetcher at EML2. At EML2 .4 km/s suffices to drop to a perigee deep in earth's gravity well. Once at perigee, .2 km/s suffices to send the fetcher on its way toward the target asteroid. A .2 km/s burn would not take long, trans asteroid injection could be achieved while still in the perigee neighborhood. After the EDS detaches from the fetcher, it would do another the .2 km/s burn to shed velocity and return to an elliptical orbit about the earth. Then the Earth Departure Stage could return to EML2 to be refueled and send another fetcher on its way.
With propellant mines in the lunar cold traps and metal mines in lunar orbit, there would be economic incentive to develop Closed Ecological Life Support (CELS). Plants to provide oxygen and food, bacteria to break down wastes. With better CELS, long trips and long stays on other bodies become more plausible. If life support materials come the moon's shallow gravity well, it is also possible to leave with more water, food and air. The life support consumables in a Zubrin style Mars Transfer Vehicle are bleeding edge minimum mass. If a CO2 scrubber or other life support mechanism breaks down, the astronauts are dead. A ship stocked with abundant water, air and food is less vulnerable to these catastrophic failure modes.
Lunar life support consumables make long trips doable. Lunar propellant would shorten trip times and expand launch windows. The revisit issue becomes less of a show stopper. It would open the door to exploiting the larger NEAs and those asteroids a little more more distant in terms of delta V.
Propellant and a staging platform at EML2 takes about 2.7 km/s off an Mars Transfer Vehicle's (MTV's) delta V budget. Or 5.4 km/s off a round trip. This smaller delta V budget allows a larger mass fraction. A larger mass fraction makes reusable MTVs more doable. As I mentioned at the start, single use $10 billion vehicles are a show stopper for establishing a Mars settlement.
A tether anchored on Phobos could be a way station to the Main Belt.
The foot of the Phobos elevator illustrated above is only .6 km/s from Mars' surface. Only .6 km/s from Mars' abundant CO2, argon and water. And from Mars' extensive mineral resources.
Elevator regions above Phobs can help receive or send payloads to or from Earth. Or the Main Belt. Or even Near Earth Asteroids. Dennis Wingo argues Mars infra-structure would open up a whole new set of launch windows to the asteroids. A whole new set of launch windows would dramatically cut revisit times to NEAs as well Main Belt asteroids.
Do we even need a 3-legged stool?
Wingo's
Moonrush takes a look at
The Club of Rome. As early as 1968 this group foresaw a major challenge: So long as we're trapped on earth, there is a ceiling to our economic growth. Unless we can break free of our cradle, we're doomed to decline or stagnation. Wingo notes space offers a much larger body of resources than our planet's surface.
We can't go very far into earth's surface before pressure and heat prevent us from going deeper. Available resources and real estate can be measured in area. The surface area of the asteroids is hundreds of thousands times that of earth. Not only is an asteroid's surface accessible but it's entire volume. Access to the asteroids would raise our ceiling many stories and we could enjoy growth for generations to come.
Tom Murphy echoes the Club of Rome warnings. Murphy is a 21st century voice warning us exponential growth isn't sustainable. Like the Club of Rome, Murphy exhorts us to conserve resources, slow population growth and live within our means. I wholeheartedly agree with this sound advice. Even if space resources were available, we should take good care of our cradle Earth.
But Murphy also argues space resources aren't practical. See
Why Not Space? and
Stranded Resources. Murphy believes the possibility of space resources will lull us into complacency and ignore the urgency of his message. So he sets out from the start to demonstrate his preconceived notion. This approach leads to some
embarrassingly bad math.
Neil DeGrasse Tyson notes NASA's funding is small fraction of our budget, less than half a penny on the dollar. He calls for 1% or a
penny for NASA. But what is the purpose of our space program? Is it to find bacteria on Mars? To plant a flag and footprints on an asteroid and return home? If that's the goal, NASA's not worth even .4% of our budget.
But if NASA could help open the gates to an endless frontier, it would be worth much more. How much is escape from our prison worth? I'd say a dime or even a quarter. Many voters would agree. But more and more voters question whether it's even possible to open the space frontier. Like Murphy, they've resigned themselves to a future where mankind is trapped beneath low earth orbit.
Zubrin, Spudis, and Lewis and like minded people should not be fighting each other. They should be working together for a common goal. And fighting the common enemy, those who have resigned themselves to stagnation.