This is a continuation of Travel on Airless Worlds where I looked at suborbital hops.
The surface of airless worlds will be exposed to radiation so it's likely the inhabitants would live underground.
Moreover, it is not as hard to burrow. The deepest gold mine on earth goes down about 4 kilometers. The heat and immense pressure make it hard to dig deeper. In contrast, the entire volume of a small body can be reached.
Courtney Seligman shows how to compute the pressure of a body with uniform density. The bodies we look at don't have uniform density but we'll use his method as a first order approximation.
Central pressure of a spherical body with uniform density is 3 g2/(8 π G)
Where G is universal gravitation constant, g is body's surface gravity and R is body's radius.
At distance r from center, pressure is (1 - (r/R)^2) * central pressure.
What is the pressure 4 kilometers below earth's surface?
Earths's radius R is 6378000 meters. r is that number minus 4000 meters. g is about 9.8 meters/sec^2.
Plugging those numbers into
(1 - (r/R)^2) * 3 g2/(8 π G)
gives 2120 atmospheres.
Besides pressure, heat also discourages us from burrowing deeper. So it might be possible to dig deeper on cooler worlds but for now we'll use 2120 atmospheres as the limit beyond which we can't dig.
3/(8 π G) * g * R2 gives different central pressures for various worlds:
Ceres center is 1430 atmospheres, well below our 2120 atmosphere limit. And Ceres is a cooler world than earth. We would be able to tunnel clear through the largest asteroid in the main belt. Since smaller asteroids would have smaller central pressure, we would be able to tunnel through the centers of every asteroid in the main belt.
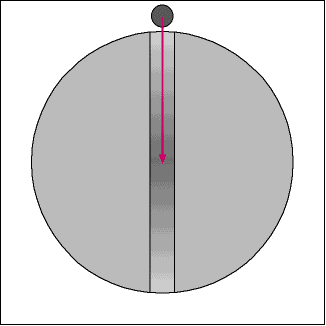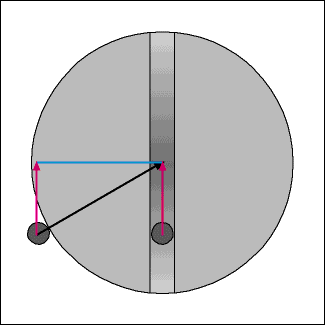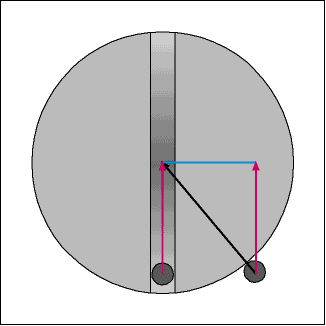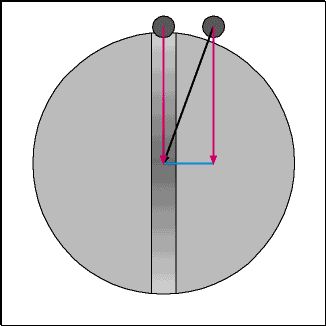
Imagine a mohole going from a body's north pole to south pole:
The diagram above breaks the acceleration vector into vertical and horizontal components. The mohole payload has the same vertical acceleration components as an object in a circular orbit with orbital radius R, R being body radius.
Somone jumping into this mohole could travel to the opposite pole for zero energy. Trip time would be the orbital period: 2 π sqrt(R3/μ).
Other chords besides a diameter could be burrowed. I like to imagine 12 subway stations corresponding to the vertices of an icosahedron:
The red subway lines to nearest neighbors would correspond to the 30 edges of an icosahedron .
Green subway lines to the next nearest neighbors would correspond to the 30 edges of a small stellated dodecahedron.
And there could be 6 diameter subway lines linking a station to stations to their antipodes.
The energy free travel time of all these lines would be the same as the diameter trip time:
2 π sqrt(R3/μ).
It would be possible have a faster trip time than 2 π sqrt(R3/μ). A train could be accelerated during the first half of the trip and decelerated the second half. During the second half, energy could be recovered using regenerative braking.
Most of small bodies in our solar system have internal pressures that don't prohibit access. But in some cases central pressure exceeds 2120 atmospheres. We'd be able to burrow only so deep. Here's my guesstimate of the maximum depth for various bodies:
Luna 40 kilometers
Mars 15 kilometers
Ganymede 77 kilometers
Callisto 97 kilometers
Europa 55 kilometers
Titania 318 kilometers
Oberon 61 kilometers
Pluto 200 kilometers
Haumea 82 kilometers
Eris 108 kilometers
Here is the spreadsheet I used to look at internal pressures.
The top four kilometers of earth's surface is only a tiny fraction of the accessible mass in our solar system.
Standup Maths did a nice look at moholes going through a body.